Πώς λειτουργούν οι μετασχηματιστές

Σύμφωνα με τον ορισμό που δίνεται στο Βικιπαίδεια ένας ηλεκτρικός μετασχηματιστής είναι ένας σταθερός εξοπλισμός που ανταλλάσσει ηλεκτρική ισχύ σε μερικά στενά πηνία, μέσω μαγνητικής επαγωγής.

Ένα συνεχώς μεταβαλλόμενο ρεύμα σε μια περιέλιξη του μετασχηματιστή δημιουργεί μια μεταβαλλόμενη μαγνητική ροή, η οποία, κατά συνέπεια, προκαλεί μια μεταβαλλόμενη ηλεκτροκινητική δύναμη πάνω από ένα δεύτερο πηνίο που χτίζεται πάνω στον ίδιο πυρήνα.

Βασική αρχή εργασίας

Οι μετασχηματιστές λειτουργούν βασικά μεταφέροντας ηλεκτρική ισχύ μεταξύ ενός ζεύγους πηνίων μέσω αμοιβαίας επαγωγής, χωρίς να εξαρτάται από οποιαδήποτε μορφή άμεσης επαφής μεταξύ των δύο περιελίξεων.

Αυτή η διαδικασία μεταφοράς ηλεκτρικής ενέργειας μέσω επαγωγής αποδείχθηκε για πρώτη φορά από τον νόμο επαγωγής του Faraday, το έτος 1831. Σύμφωνα με αυτόν τον νόμο, η επαγόμενη τάση σε δύο πηνία δημιουργείται λόγω μιας διαφορετικής μαγνητικής ροής που περιβάλλει το πηνίο.

Η θεμελιώδης λειτουργία ενός μετασχηματιστή είναι να ανεβείτε ή να κατεβείτε εναλλασσόμενη τάση / ρεύμα, σε διαφορετικές αναλογίες σύμφωνα με την απαίτηση της εφαρμογής. Οι αναλογίες αποφασίζονται από τον αριθμό των στροφών και την αναλογία στροφής της περιέλιξης.

Ανάλυση ενός ιδανικού μετασχηματιστή

Μπορούμε να φανταστούμε έναν ιδανικό μετασχηματιστή να είναι υποθετικός σχεδιασμός που μπορεί να είναι ουσιαστικά χωρίς καμία μορφή απώλειας. Επιπλέον, αυτός ο ιδανικός σχεδιασμός μπορεί να έχει την πρωτεύουσα και τη δευτερεύουσα περιέλιξη τέλεια σε συνδυασμό μεταξύ τους.

Αυτό σημαίνει ότι η μαγνητική σύνδεση μεταξύ των δύο περιελίξεων είναι μέσω ενός πυρήνα του οποίου η μαγνητική διαπερατότητα είναι άπειρη και με επαγωγικές περιελίξεις με συνολική μηδενική μαγνητοκινητική δύναμη.

Γνωρίζουμε ότι σε έναν μετασχηματιστή, το εφαρμοζόμενο εναλλασσόμενο ρεύμα στην πρωτεύουσα περιέλιξη προσπαθεί να επιβάλει μια διαφορετική μαγνητική ροή εντός του πυρήνα του μετασχηματιστή, η οποία περιλαμβάνει επίσης τη δευτερεύουσα περιέλιξη που περιβάλλεται γύρω από αυτόν.

Λόγω αυτής της μεταβαλλόμενης ροής, προκαλείται μια ηλεκτροκινητική δύναμη (EMF) στη δευτερεύουσα περιέλιξη μέσω ηλεκτρομαγνητικής επαγωγής. Αυτό έχει ως αποτέλεσμα τη δημιουργία ροής στη δευτερεύουσα περιέλιξη με μέγεθος αντίθετο αλλά ίσο με την πρωτογενή ροή περιέλιξης, σύμφωνα με Ο νόμος του Lenz'z .

Δεδομένου ότι ο πυρήνας φέρει άπειρη μαγνητική διαπερατότητα, ολόκληρη η (100%) μαγνητική ροή μπορεί να μεταφερθεί κατά μήκος των δύο περιελίξεων.

Αυτό υπονοεί ότι, όταν το πρωτεύον υποβάλλεται σε πηγή εναλλασσόμενου ρεύματος και ένα φορτίο συνδέεται με τους δευτερεύοντες ακροδέκτες περιέλιξης, το ρεύμα ρέει μέσω της αντίστοιχης περιέλιξης σε κατευθύνσεις όπως υποδεικνύεται στο ακόλουθο διάγραμμα. Σε αυτήν την κατάσταση, η μαγνητική κινητική δύναμη του πυρήνα εξουδετερώνεται στο μηδέν.

Η εικόνα είναι ευγενική προσφορά: https://commons.wikimedia.org/wiki/File:Transformer3d_col3.svg

Σε αυτόν τον ιδανικό σχεδιασμό μετασχηματιστή, δεδομένου ότι η μεταφορά ροής στην πρωτεύουσα και δευτερεύουσα περιέλιξη είναι 100%, σύμφωνα με τον νόμο του Faraday, η επαγόμενη τάση σε κάθε τύλιγμα θα είναι απόλυτα ανάλογη με τον αριθμό στροφών της περιέλιξης, όπως φαίνεται στα παρακάτω εικόνα:

Δοκιμή βίντεο επαλήθευση της γραμμικής σχέσης μεταξύ του λόγου πρωτοβάθμιας / δευτεροβάθμιας στροφής.

ΣΤΡΟΦΕΣ ΚΑΙ ΡΑΤΙΕΣ ΤΑΣΗΣ

Ας προσπαθήσουμε να κατανοήσουμε λεπτομερώς τους υπολογισμούς της αναλογίας στροφής:

Το καθαρό μέγεθος της τάσης που προκαλείται από την πρωτογενή προς τη δευτερεύουσα περιέλιξη καθορίζεται απλώς από την αναλογία του αριθμού των στροφών που τυλίγονται πάνω από τα πρωτεύοντα και τα δευτερεύοντα τμήματα.

Ωστόσο, αυτός ο κανόνας ισχύει μόνο εάν ο μετασχηματιστής βρίσκεται κοντά σε έναν ιδανικό μετασχηματιστή.

Ένας ιδανικός μετασχηματιστής είναι αυτός ο μετασχηματιστής που έχει αμελητέες απώλειες με τη μορφή της επιδερμίδας ή του ρεύματος.

Ας πάρουμε το παράδειγμα του σχήματος 1 παρακάτω (για έναν ιδανικό μετασχηματιστή).

Ας υποθέσουμε ότι η πρωτεύουσα περιέλιξη αποτελείται από περίπου 10 στροφές, ενώ η δευτερεύουσα με μία μόνο στροφή. Λόγω της ηλεκτρομαγνητικής επαγωγής, οι γραμμές ροής που δημιουργούνται κατά μήκος της πρωτεύουσας περιέλιξης σε απόκριση στο εισερχόμενο AC, εναλλάσσονται και καταρρέουν εναλλάξ, περνώντας τις 10 στροφές της πρωτεύουσας περιέλιξης. Αυτό οδηγεί σε επακριβώς αναλογική ποσότητα τάσης που προκλήθηκε κατά τη δευτερεύουσα περιέλιξη ανάλογα με την αναλογία στροφής.

Η περιέλιξη που παρέχεται με είσοδο AC γίνεται η κύρια περιέλιξη, ενώ η συμπληρωματική περιέλιξη που παράγει την έξοδο μέσω μαγνητικής επαγωγής από την πρωτεύουσα γίνεται η δευτερεύουσα περιέλιξη.

Φιγούρα 1)

Δεδομένου ότι το δευτερεύον έχει μόνο μία στροφή, βιώνει μια αναλογική μαγνητική ροή σε μία στροφή σε σχέση με τις 10 στροφές του πρωτεύοντος.

Επομένως, δεδομένου ότι η τάση που εφαρμόζεται στο πρωτεύον είναι 12 V, τότε κάθε τύλιγμα θα υποβληθεί με μετρητή EMF 12/10 = 1,2 V, και αυτό είναι ακριβώς το μέγεθος της τάσης που θα επηρέαζε την απλή στροφή που υπάρχει το δευτερεύον τμήμα. Αυτό συμβαίνει επειδή έχει ένα μόνο τύλιγμα το οποίο είναι ικανό να εξαγάγει μόνο την ίδια ισοδύναμη ποσότητα επαγωγής που μπορεί να είναι διαθέσιμη σε όλη τη στροφή πάνω από την πρωτεύουσα.

Έτσι, το δευτερεύον με μία στροφή θα μπορούσε να εξαγάγει 1.2V από το πρωτεύον.

Η παραπάνω εξήγηση δείχνει ότι ο αριθμός των στροφών πάνω από ένα πρωτεύον μετασχηματιστή αντιστοιχεί γραμμικά με την τάση τροφοδοσίας απέναντί ​​του και η τάση απλώς διαιρείται με τον αριθμό των στροφών.

Έτσι, στην παραπάνω περίπτωση, δεδομένου ότι η τάση είναι 12V, και ο αριθμός στροφών είναι 10, ο καθαρός μετρητής EMF που προκαλείται σε κάθε μία από τις στροφές θα ήταν 12/10 = 1.2V

Παράδειγμα # 2

Τώρα ας απεικονίσουμε το σχήμα 2 παρακάτω, δείχνει έναν παρόμοιο τύπο διαμόρφωσης όπως στο σχήμα 1. περιμένετε το δευτερεύον που έχει τώρα 1 επιπλέον στροφή, δηλαδή 2 αριθμούς στροφών.

Περιττό να πούμε, ότι τώρα το δευτερεύον θα περνούσε δύο φορές περισσότερες γραμμές ροής σε σύγκριση με την κατάσταση 1 που είχε μόνο μία στροφή.

Εδώ λοιπόν η δευτερεύουσα περιέλιξη θα διάβαζε περίπου 12/10 x 2 = 2.4V, επειδή οι δύο στροφές θα επηρεαστούν από ένα μέγεθος μετρητή EMF που μπορεί να είναι ισοδύναμο στις δύο περιελίξεις στην πρωτεύουσα πλευρά του trafo.

Επομένως, από την παραπάνω συζήτηση γενικά μπορούμε να συμπεράνουμε ότι σε έναν μετασχηματιστή η σχέση μεταξύ της τάσης και του αριθμού των στροφών στο πρωτεύον και το δευτερεύον είναι αρκετά γραμμική και ανάλογη.

Αριθμοί στροφής μετασχηματιστή

Έτσι, ο παράγοντας που προκύπτει για τον υπολογισμό του αριθμού στροφών για κάθε μετασχηματιστή μπορεί να εκφραστεί ως:

Es / Ep = Ns / Np

που,

• Es = Δευτερεύουσα τάση ,
• Ep = Πρωτεύουσα τάση,
• Ns = Αριθμός δευτερευουσών στροφών,
• Np = Αριθμός κύριων στροφών.

Κύριος λόγος δευτερογενούς στροφής

Θα ήταν ενδιαφέρον να σημειωθεί ότι ο παραπάνω τύπος υποδεικνύει μια απλή σχέση μεταξύ του λόγου της δευτερεύουσας προς την πρωτογενή τάση και της δευτεροβάθμιας προς τον πρωτεύοντα αριθμό στροφών, οι οποίες υποδεικνύονται ότι είναι αναλογικές και ίσες.

Επομένως, η παραπάνω εξίσωση μπορεί επίσης να εκφραστεί ως:

Ep x Ns = Es x Np

Στη συνέχεια, μπορούμε να αντλήσουμε τον παραπάνω τύπο για την επίλυση των Es και Ep όπως φαίνεται παρακάτω:

Es = (Ep x Ns) / Np

ομοίως,

Ep = (Es x Np) / Ns

Η παραπάνω εξίσωση δείχνει ότι εάν υπάρχουν 3 μεγέθη, το τέταρτο μέγεθος θα μπορούσε εύκολα να προσδιοριστεί με την επίλυση του τύπου.

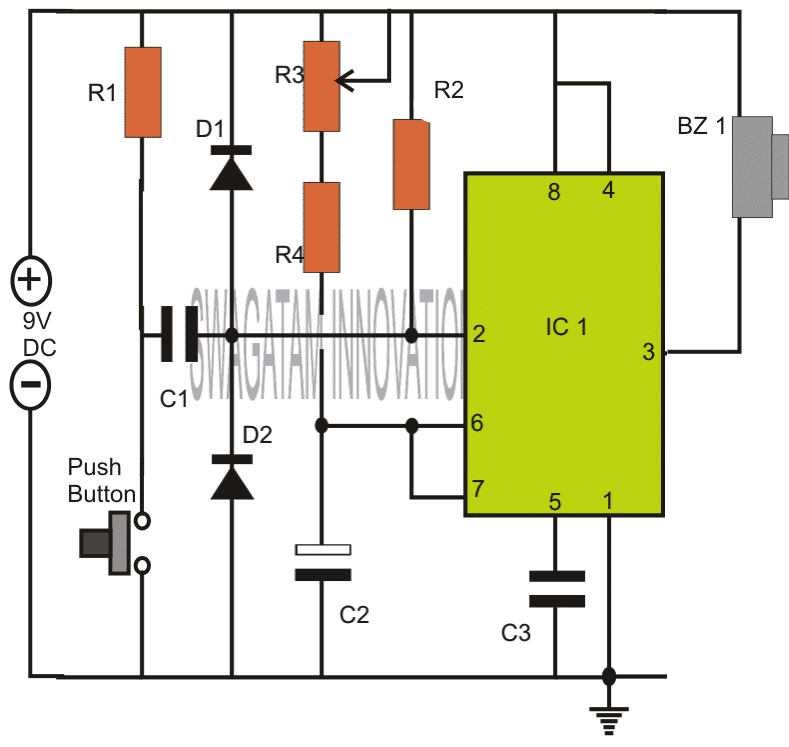
Επίλυση προβλημάτων πρακτικής περιέλιξης μετασχηματιστή

Περίπτωση στο σημείο # 1: Ένας μετασχηματιστής διαθέτει 200 ​​αριθμό στροφών στο πρωτεύον τμήμα, 50 αριθμό στροφών στο δευτερεύον και 120 βολτ συνδεδεμένα κατά μήκος του πρωτεύοντος (Ep). Ποια θα μπορούσε να είναι η τάση στο δευτερεύον (E);

Δεδομένος:

• Np = 200 στροφές
• Ns = 50 στροφές
• Ep = 120 βολτ
• Είναι =; βολτ

Απάντηση:

Es = EpNs / Np

Αντικατάσταση:

Es = (120V x 50 στροφές) / 200 στροφές

Es = 30 βολτ

Περίπτωση στο σημείο # 2 : Ας υποθέσουμε ότι έχουμε 400 στροφές καλωδίων σε πηνίο σιδήρου-πυρήνα.

Υποθέτοντας ότι το πηνίο πρέπει να χρησιμοποιηθεί ως η πρωτεύουσα περιέλιξη ενός μετασχηματιστή, Υπολογίστε τον αριθμό των στροφών που πρέπει να τυλιχτούν στο πηνίο για να αποκτήσετε τη δευτερεύουσα περιέλιξη του μετασχηματιστή για να εξασφαλίσετε μια δευτερεύουσα τάση ενός βολτ με μια κατάσταση όπου η κύρια η τάση είναι 5 βολτ;

Δεδομένος:

• Np = 400 στροφές
• Ep = 5 βολτ
• Es = 1 βολτ
• Ns =? στροφές

Απάντηση:

EpNs = EsNp

Μεταφορά για Ns:

Ns = EsNp / Επ

Αντικατάσταση:

Ns = (1V x 400 στροφές) / 5 βολτ

Ns = 80 στροφές

Εχε υπόψιν: Η αναλογία της τάσης (5: 1) είναι ισοδύναμη με την αναλογία περιέλιξης (400: 80). Περιστασιακά, ως υποκατάστατο συγκεκριμένων τιμών, βρίσκεστε στον εαυτό σας με αναλογία στροφής ή τάσης.

Σε τέτοιες περιπτώσεις, θα μπορούσατε απλά να υποθέσετε οποιονδήποτε αυθαίρετο αριθμό για μία από τις τάσεις (ή περιέλιξη) και να υπολογίσετε την άλλη εναλλακτική τιμή από την αναλογία.

Για παράδειγμα, ας υποθέσουμε ότι ο λόγος περιέλιξης αντιστοιχεί σε 6: 1, θα μπορούσατε να φανταστείτε μια ποσότητα στροφής για το πρωτεύον τμήμα και να υπολογίσετε τον ισοδύναμο δευτερεύοντα αριθμό στροφών, χρησιμοποιώντας παρόμοιες αναλογίες όπως 60:10, 36: 6, 30: 5 κ.λπ.

Ο μετασχηματιστής σε όλα τα παραπάνω παραδείγματα φέρει μικρότερο αριθμό στροφών στο δευτερεύον τμήμα σε σύγκριση με το πρωτεύον τμήμα. Για αυτόν τον λόγο, μπορείτε να βρείτε μικρότερη ποσότητα τάσης στο δευτερεύον του trafo και όχι στην κύρια πλευρά.

Τι είναι οι μετασχηματιστές Step-up και Step-Down

Ένας μετασχηματιστής που έχει βαθμολογία δευτερεύουσας πλευρικής τάσης χαμηλότερη από την αρχική βαθμολογία πλευρικής τάσης αναφέρεται ως α Μετασχηματιστής STEP-DOWN .

Ή, εναλλακτικά, εάν η είσοδος AC εφαρμόζεται στην περιέλιξη που έχει μεγαλύτερο αριθμό στροφών, τότε ο μετασχηματιστής ενεργεί σαν μετασχηματιστής κατεβάσματος.

Ο λόγος ενός μετασχηματιστή step-down από τέσσερα προς ένα γράφεται ως 4: 1. Ένας μετασχηματιστής που περιλαμβάνει μικρότερο αριθμό στροφών στην πρωτεύουσα πλευρά σε σύγκριση με τη δευτερεύουσα πλευρά θα παράγει υψηλότερη τάση κατά μήκος της δευτερεύουσας πλευράς σε σύγκριση με την τάση που συνδέεται κατά μήκος της πρωτεύουσας πλευράς.

Ένας μετασχηματιστής ο οποίος έχει μια δευτερεύουσα πλευρά ονομασμένος πάνω από την τάση κατά μήκος της πρωτεύουσας πλευράς αναφέρεται ως μετασχηματιστής STEP-UP. Ή, εναλλακτικά, εάν η είσοδος AC εφαρμόζεται σε μια περιέλιξη που έχει μικρότερο αριθμό στροφών, τότε ο μετασχηματιστής ενεργεί σαν ένας μετασχηματιστής ενίσχυσης.

Η αναλογία ενός μετασχηματιστή step-up με ένα προς τέσσερα πρέπει να εγγραφεί ως 1: 4. Όπως μπορείτε να δείτε στις δύο αναλογίες ότι το μέγεθος της πρωτεύουσας πλευρικής περιέλιξης αναφέρεται με συνέπεια στην αρχή.

Μπορούμε να χρησιμοποιήσουμε ένα μετασχηματιστή Step-down ως μετασχηματιστή Step-up και Vice Versa;

Ναι σίγουρα! Όλοι οι μετασχηματιστές λειτουργούν με την ίδια θεμελιώδη αρχή όπως περιγράφεται παραπάνω. Η χρήση ενός μετασχηματιστή step-up ως μετασχηματιστή step-down σημαίνει απλώς την εναλλαγή των τάσεων εισόδου στην κύρια / δευτερεύουσα περιέλιξή τους.

Για παράδειγμα, εάν έχετε έναν συνηθισμένο μετασχηματιστή τροφοδοσίας που σας παρέχει έξοδο 12-0-12V από εναλλασσόμενο ρεύμα 220V, μπορείτε να χρησιμοποιήσετε τον ίδιο μετασχηματιστή με έναν μετασχηματιστή αύξησης για παραγωγή 220V εξόδου από 12V AC εισαγωγή.

Ένα κλασικό παράδειγμα είναι ένα κύκλωμα μετατροπέα , όπου οι μετασχηματιστές δεν έχουν τίποτα ιδιαίτερο σε αυτά. Όλοι λειτουργούν χρησιμοποιώντας τους συνηθισμένους μετασχηματιστές step-down που συνδέονται με τον αντίθετο τρόπο.

Αντίκτυπος φορτίου

Κάθε φορά που ένα φορτίο ή μια ηλεκτρική συσκευή συνδέεται στη δευτερεύουσα περιέλιξη ενός μετασχηματιστή, το ρεύμα ή οι ενισχυτές διατρέχουν τη δευτερεύουσα πλευρά της περιέλιξης μαζί με το φορτίο.

Η μαγνητική ροή που παράγεται από το ρεύμα στη δευτερεύουσα περιέλιξη αλληλεπιδρά με τις μαγνητικές γραμμές ροής που παράγονται από τους ενισχυτές στην κύρια πλευρά. Αυτή η σύγκρουση μεταξύ των δύο γραμμών ροής δημιουργείται ως αποτέλεσμα της κοινής επαγωγής μεταξύ της πρωτεύουσας και της δευτερεύουσας περιέλιξης.

Αμοιβαία ροή

Η απόλυτη ροή στο υλικό πυρήνα του μετασχηματιστή επικρατεί τόσο στην πρωτεύουσα όσο και στη δευτερεύουσα περιέλιξη. Είναι επίσης ένας τρόπος μέσω του οποίου η ηλεκτρική ενέργεια μπορεί να μετακινηθεί από το πρωτεύον τύλιγμα στο δευτερεύον τύλιγμα.

Λόγω του γεγονότος ότι αυτή η ροή ενώνει και τις δύο περιελίξεις, το φαινόμενο είναι γενικά γνωστό ως MUTUAL FLUX. Επίσης, η επαγωγή που δημιουργεί αυτή τη ροή είναι διαδεδομένη και στις δύο περιελίξεις και ονομάζεται αμοιβαία επαγωγή.

Το σχήμα (2) παρακάτω δείχνει τη ροή που δημιουργείται από τα ρεύματα στην πρωτεύουσα και δευτερεύουσα περιέλιξη ενός μετασχηματιστή κάθε φορά που το ρεύμα τροφοδοσίας ενεργοποιείται στην πρωτεύουσα περιέλιξη.

Σχήμα 2)

Κάθε φορά που η αντίσταση φορτίου συνδέεται στη δευτερεύουσα περιέλιξη, η τάση που διεγείρεται στη δευτερεύουσα περιέλιξη ενεργοποιεί το ρεύμα να κυκλοφορεί στη δευτερεύουσα περιέλιξη.

Αυτό το ρεύμα παράγει ένα δακτύλιο ροής γύρω από τη δευτερεύουσα περιέλιξη (υποδεικνύεται ως διακεκομμένες γραμμές) που μπορεί να είναι εναλλακτικά του πεδίου ροής γύρω από το πρωτεύον (νόμος του Lenz).

Κατά συνέπεια, η ροή γύρω από τη δευτερεύουσα περιέλιξη ακυρώνει το μεγαλύτερο μέρος της ροής γύρω από την πρωτεύουσα περιέλιξη.

Με μικρότερη ποσότητα ροής που περιβάλλει την πρωτεύουσα περιέλιξη, η αντίστροφη emf κόβεται και απορροφάται περισσότερος ενισχυτής από την παροχή. Το συμπληρωματικό ρεύμα στην πρωτεύουσα περιέλιξη απελευθερώνει πρόσθετες γραμμές ροής, αποκαθιστώντας σχεδόν την αρχική ποσότητα γραμμών απόλυτης ροής.

ΓΥΝΑΙΚΕΙΑ ΚΑΙ ΤΡΕΧΟΝΤΟΣ ΡΑΤΙΟΣ

Η ποσότητα των γραμμών ροής που παράγονται σε έναν πυρήνα trafo είναι ανάλογη της μαγνητικής δύναμης

(ΣΕ ΑΜΠΕΡ-ΓΥΡΕΣ) των πρωτογενών και δευτερευόντων περιελίξεων.

Η στροφή του αμπέρ (I x N) είναι ενδεικτική της κινητικής δύναμης που μπορεί να γίνει κατανοητή ως η μαγνητοκινητική δύναμη που παράγεται από ένα αμπέρ ρεύματος που λειτουργεί σε ένα πηνίο 1 στροφής.

Η ροή που διατίθεται στον πυρήνα ενός μετασχηματιστή περιβάλλει τις πρωτεύουσες και δευτερεύουσες περιελίξεις.

Δεδομένου ότι η ροή είναι πανομοιότυπη για κάθε περιέλιξη, οι στροφές των αμπέρ σε κάθε, η πρωτεύουσα και η δευτερεύουσα περιέλιξη πρέπει πάντα να είναι οι ίδιες.

Για αυτόν τον λόγο:

IpNp = IsNs

Που:

IpNp = ampere / στροφές στην πρωτεύουσα περιέλιξη
IsNs - αμπέρ / στροφές στη δευτερεύουσα περιέλιξη

Διαιρώντας και τις δύο πλευρές της έκφρασης με
Ιπ , παίρνουμε:
Np / Ns = Is / Ip

Από: Es / Ep = Ns / Np

Επειτα: Ep / Es = Np / Ns

Επίσης: Ep / Es = Is / Ip

που

• Ep = τάση που εφαρμόζεται σε πρωτογενή σε βολτ
• Es = τάση κατά μήκος του δευτερεύοντος σε βολτ
• Ip = ρεύμα στο πρωτεύον στο Amp
• Is = τρέχουσα στη δευτερεύουσα στο Amps

Παρατηρήστε ότι οι εξισώσεις υποδεικνύουν την αναλογία αμπέρ να είναι το αντίστροφο του λόγου περιέλιξης ή περιστροφής καθώς και το λόγο τάσης.

Αυτό σημαίνει, ένας μετασχηματιστής που διαθέτει λιγότερους αριθμούς στροφών στη δευτερεύουσα πλευρά σε σύγκριση με τον πρωτεύοντα μπορεί να κατεβάσει την τάση, αλλά θα αυξήσει το ρεύμα. Για παράδειγμα:

Ένας μετασχηματιστής υποτίθεται ότι έχει λόγο τάσης 6: 1.

Προσπαθήστε να βρείτε το ρεύμα ή ενισχυτές στη δευτερεύουσα πλευρά εάν το ρεύμα ή ενισχυτής στην κύρια πλευρά είναι 200 ​​χιλιοστά.

Υποθέτω

Ep = 6V (για παράδειγμα)
Είναι = 1V
Ip = 200mA ή 0,2Amps
Είναι =;

Απάντηση:

Ep / Es = Is / Ip

Μεταφορά για είναι:

Is = EpIp / Es

Αντικατάσταση:

Is = (6V x 0.2A) / 1V
Είναι = 1.2Α

Το παραπάνω σενάριο αναφέρεται ότι παρά το γεγονός ότι η τάση κατά μήκος της δευτερεύουσας περιέλιξης είναι το ένα έκτο της τάσης κατά μήκος της πρωτεύουσας περιέλιξης, οι ενισχυτές στη δευτερεύουσα περιέλιξη είναι 6 φορές οι ενισχυτές στην πρωτεύουσα περιέλιξη.

Οι παραπάνω εξισώσεις θα μπορούσαν πολύ καλά να εξεταστούν από μια εναλλακτική προοπτική.

Η αναλογία περιέλιξης υποδηλώνει το άθροισμα μέσω του οποίου ο μετασχηματιστής ενισχύει ή αυξάνει ή μειώνει την τάση που συνδέεται με την πρωτεύουσα πλευρά.

Ακριβώς για παράδειγμα, ας υποθέσουμε ότι εάν η δευτερεύουσα περιέλιξη ενός μετασχηματιστή έχει διπλάσιο αριθμό στροφών από την πρωτεύουσα περιέλιξη, η τάση που διεγείρεται στη δευτερεύουσα πλευρά πιθανότατα θα είναι διπλάσια από την τάση κατά μήκος της πρωτογενούς περιέλιξης.

Σε περίπτωση που η δευτερεύουσα περιέλιξη φέρει το ήμισυ του αριθμού των στροφών της πρωτεύουσας πλευράς, η τάση κατά μήκος της δευτερεύουσας πλευράς θα είναι το ήμισυ της τάσης κατά μήκος της πρωτεύουσας περιέλιξης.

Τούτου λεχθέντος, ο λόγος περιέλιξης και ο λόγος ενισχυτή ενός μετασχηματιστή περιλαμβάνουν μια αντίστροφη σχέση.

Ως αποτέλεσμα, ένας μετασχηματιστής βήματος 1: 2 θα μπορούσε να έχει το μισό ενισχυτή στη δευτερεύουσα πλευρά σε σύγκριση με την πρωτεύουσα πλευρά. Ένας μετασχηματιστής 2: 1 μπορεί να έχει διπλάσιο ενισχυτή στη δευτερεύουσα περιέλιξη σε σχέση με την πρωτεύουσα πλευρά.

Απεικόνιση: Ένας μετασχηματιστής με αναλογία περιέλιξης 1:12 διαθέτει 3 αμπέρ ρεύματος στη δευτερεύουσα πλευρά. Μάθετε το μέγεθος των ενισχυτών στην κύρια περιέλιξη;

Δεδομένος:

Np = 1 στροφή (για παράδειγμα)
Ns = 12 στροφές
Είναι = 3Amp
Lp =?

Απάντηση:

Np / Ns = Is / Ip

Αντικατάσταση:

Ip = (12 στροφές x 3 Amp) / 1 στροφή

Ip = 36Α

Υπολογισμός αμοιβαίας επαγωγής

Η αμοιβαία επαγωγή είναι μια διαδικασία κατά την οποία μια περιέλιξη διέρχεται από μια επαγωγή EMF λόγω του ρυθμού αλλαγής ρεύματος της παρακείμενης περιέλιξης που οδηγεί σε επαγωγική σύζευξη μεταξύ της περιέλιξης.

Με άλλα λόγια Αμοιβαία επαγωγή είναι ο λόγος του επαγόμενου emf σε μια περιέλιξη προς τον ρυθμό μεταβολής του ρεύματος στην άλλη περιέλιξη, όπως εκφράζεται στον ακόλουθο τύπο:

M = emf / di (t) / dt

Φάση στα Transformers:

Κανονικά, όταν εξετάζουμε μετασχηματιστές, οι περισσότεροι από εμάς πιστεύουν ότι η πρωτογενής και δευτερεύουσα τάση και ρεύματα περιέλιξης βρίσκονται σε φάση μεταξύ τους. Ωστόσο, αυτό μπορεί να μην είναι πάντα αλήθεια. Στους μετασχηματιστές, η σχέση μεταξύ της τάσης, της τρέχουσας γωνίας φάσης σε πρωτογενή και δευτερεύουσα βασίζεται στο πώς αυτές οι περιελίξεις περιστρέφονται γύρω από τον πυρήνα. Εξαρτάται από το αν είναι και οι δύο σε αριστερόστροφη κατεύθυνση, ή δεξιόστροφα ή μπορεί το ένα τύλιγμα να περιστραφεί δεξιόστροφα, ενώ το άλλο τυλίγει αριστερόστροφα.

Ας δούμε τα ακόλουθα διαγράμματα για να κατανοήσουμε πώς ο προσανατολισμός της περιέλιξης επηρεάζει τη γωνία φάσης:

Στο παραπάνω παράδειγμα, οι κατευθύνσεις περιέλιξης φαίνονται πανομοιότυπες, δηλαδή η πρωτεύουσα και η δευτερεύουσα περιέλιξη στρέφονται προς τη φορά των δεικτών του ρολογιού. Λόγω αυτού του ίδιου προσανατολισμού, η γωνία φάσης του ρεύματος εξόδου και της τάσης είναι ίδια με τη γωνία φάσης του ρεύματος εισόδου και της τάσης.

Στο δεύτερο παράδειγμα παραπάνω, η κατεύθυνση περιέλιξης του μετασχηματιστή μπορεί να φανεί τυλιγμένη με αντίθετο προσανατολισμό. Όπως φαίνεται, το πρωτεύον φαίνεται να είναι δεξιόστροφα, ενώ το δευτερεύον τυλίγεται αριστερόστροφα. Λόγω αυτού του αντίθετου προσανατολισμού περιέλιξης, η γωνία φάσης μεταξύ των δύο περιελίξεων απέχει 180 μοίρες και η επαγόμενη δευτερεύουσα έξοδος δείχνει ένα ρεύμα εκτός φάσης και απόκριση τάσης.

Dot Notation και Dot Convention

Προκειμένου να αποφευχθούν οι συγχύσεις, χρησιμοποιείται η σημείωση σημείων ή η σύμβαση Dot για την αναπαράσταση του προσανατολισμού περιέλιξης ενός μετασχηματιστή. Αυτό επιτρέπει στο χρήστη να κατανοήσει τις προδιαγραφές γωνίας φάσης εισόδου και εξόδου, είτε η πρωτεύουσα και η δευτερεύουσα περιέλιξη βρίσκονται σε φάση είτε εκτός φάσης.

Η σύμβαση κουκκίδων υλοποιείται με σημεία κουκκίδων κατά μήκος του σημείου εκκίνησης περιέλιξης, υποδεικνύοντας εάν η περιέλιξη βρίσκεται σε φάση ή εκτός φάσης μεταξύ τους.

Το ακόλουθο σχηματικό μετασχηματιστή φέρει μια ένδειξη σύμβασης κουκκίδων, και σημαίνει ότι ο πρωτεύων και ο δευτερεύων του μετασχηματιστή βρίσκονται σε φάση μεταξύ τους.

Η σημειογραφία κουκίδων που χρησιμοποιείται στην παρακάτω εικόνα δείχνει τα DOTs τοποθετημένα απέναντι από τα πρωτεύοντα και τη δευτερεύουσα περιέλιξη. Αυτό δείχνει ότι ο προσανατολισμός περιέλιξης των δύο πλευρών δεν είναι ο ίδιος και επομένως η γωνία φάσης κατά μήκος των δύο περιελίξεων θα είναι 180 μοίρες εκτός φάσης όταν εφαρμόζεται είσοδος AC σε μία από τις περιελίξεις.

Απώλειες σε πραγματικό μετασχηματιστή

Οι υπολογισμοί και οι τύποι που εξετάστηκαν στις παραπάνω παραγράφους βασίστηκαν σε έναν ιδανικό μετασχηματιστή. Ωστόσο, στον πραγματικό κόσμο, και για έναν πραγματικό μετασχηματιστή, το σενάριο μπορεί να είναι πολύ διαφορετικό.

Θα διαπιστώσετε ότι σε ιδανικό σχεδιασμό θα αγνοηθούν οι ακόλουθοι θεμελιώδεις γραμμικοί παράγοντες των πραγματικών μετασχηματιστών:

(α) Πολλοί τύποι βασικών απωλειών, γνωστοί ως μαγνητίζοντας τρέχουσες απώλειες, που μπορεί να περιλαμβάνουν τους ακόλουθους τύπους απωλειών:

• Απώλειες υστέρησης: αυτό οφείλεται σε μη γραμμικές επιδράσεις της μαγνητικής ροής στον πυρήνα του μετασχηματιστή.
• Απώλειες ρεύματος Eddy: Αυτή η απώλεια προκαλείται λόγω του φαινομένου που ονομάζεται θέρμανση joule στον πυρήνα του μετασχηματιστή. Είναι ανάλογο με το τετράγωνο της τάσης που εφαρμόζεται στο πρωτεύον του μετασχηματιστή.

(β) Σε αντίθεση με τον ιδανικό μετασχηματιστή, η αντίσταση της περιέλιξης σε πραγματικό μετασχηματιστή δεν μπορεί ποτέ να έχει μηδενική αντίσταση. Αυτό σημαίνει ότι η περιέλιξη θα έχει τελικά κάποια αντίσταση και επαγωγές που σχετίζονται με αυτές.

• Απώλειες Joule: Όπως εξηγήθηκε παραπάνω, η αντίσταση που δημιουργείται στα τερματικά περιέλιξης προκαλεί απώλειες Joule.
• Ροή διαρροής: Γνωρίζουμε ότι οι μετασχηματιστές εξαρτώνται σε μεγάλο βαθμό από τη μαγνητική επαγωγή κατά την περιέλιξή τους. Ωστόσο, δεδομένου ότι η περιέλιξη βασίζεται σε έναν κοινό πυρήνα, η μαγνητική ροή δείχνει την τάση διαρροής κατά μήκος της περιέλιξης μέσω του πυρήνα. Αυτό δημιουργεί μια σύνθετη αντίσταση που ονομάζεται πρωτογενής / δευτερεύουσα αντιδραστική αντίσταση, η οποία συμβάλλει στις απώλειες του μετασχηματιστή.

(γ) Δεδομένου ότι ένας μετασχηματιστής είναι επίσης ένα είδος επαγωγέα, επηρεάζεται επίσης από φαινόμενο όπως η παρασιτική χωρητικότητα και ο αυτο-συντονισμός, λόγω της διανομής ηλεκτρικού πεδίου. Αυτή η παρασιτική χωρητικότητα μπορεί συνήθως να είναι σε 3 διαφορετικές μορφές όπως δίνεται παρακάτω:

• Η χωρητικότητα δημιουργείται μεταξύ των στροφών το ένα πάνω στο άλλο μέσα σε ένα μόνο στρώμα
• Η χωρητικότητα δημιουργείται σε δύο ή περισσότερα παρακείμενα στρώματα
• Δημιουργείται χωρητικότητα μεταξύ του πυρήνα του μετασχηματιστή και των στρώσεων περιέλιξης που βρίσκονται δίπλα στον πυρήνα

συμπέρασμα

Από την παραπάνω συζήτηση, μπορούμε να κατανοήσουμε ότι σε πρακτικές εφαρμογές ο υπολογισμός ενός μετασχηματιστή, ειδικά ένας μετασχηματιστής σιδήρου πυρήνα μπορεί να μην είναι τόσο απλός όσο ένας ιδανικός μετασχηματιστής.

Για να λάβουμε τα πιο ακριβή αποτελέσματα για τα δεδομένα περιέλιξης, ίσως χρειαστεί να λάβουμε υπόψη πολλούς παράγοντες, όπως: πυκνότητα ροής, περιοχή πυρήνα, μέγεθος πυρήνα, πλάτος γλωττίδας, περιοχή παραθύρου, τύπος υλικού πυρήνα κ.λπ.

Μπορείτε να μάθετε περισσότερα για όλους αυτούς τους υπολογισμούς κάτω από αυτήν την ανάρτηση: