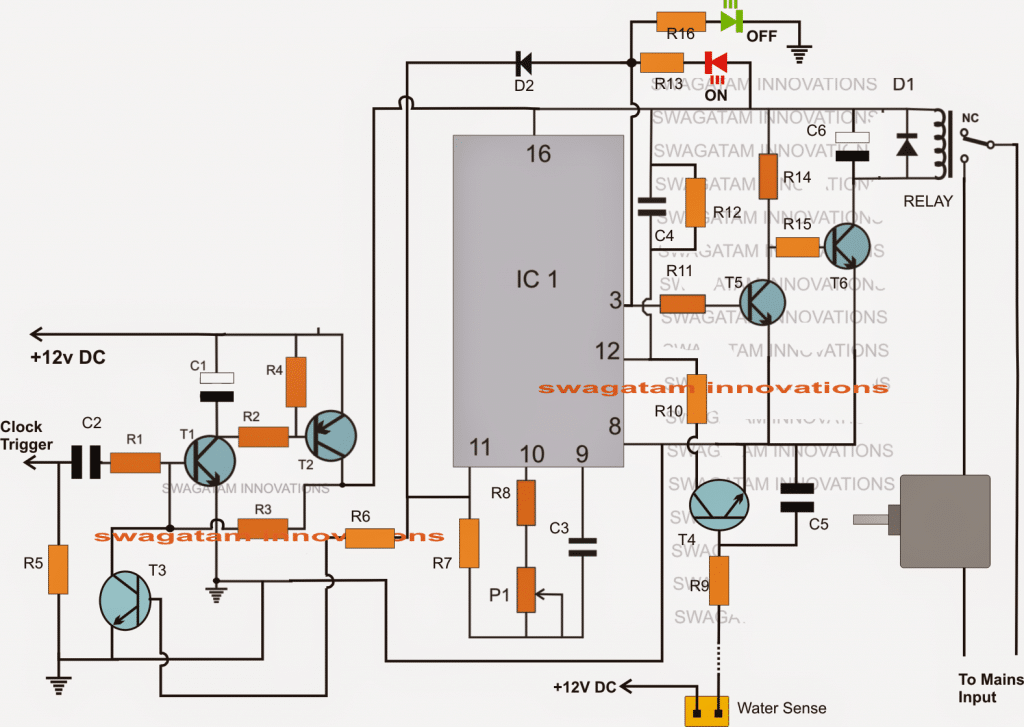
Οι διάφορες μορφές κανονικής έκφρασης που περιλαμβάνουν το άθροισμα των προϊόντων (SOP) και τα προϊόντα του αθροίσματος (POS), κανονική έκφραση μπορεί να οριστεί ως Boolean έκφραση το οποίο έχει είτε ελάχιστο όρο, διαφορετικά ανώτατο όρο Για παράδειγμα, εάν έχουμε δύο μεταβλητές, δηλαδή X & Y, τότε η κανονική έκφραση που αποτελείται από ελάχιστους όρους θα είναι XY + X'Y ', ενώ η κανονική έκφραση που περιλαμβάνει max όρους θα είναι (X + Y) (X' + Y ' ). Αυτό το άρθρο ασχολείται με μια επισκόπηση του αθροίσματος των προϊόντων και του προϊόντος των αθροισμάτων, των τύπων SOP και POS, του σχηματικού σχεδιασμού και του χάρτη K.
Άθροισμα προϊόντων και προϊόν αθροίσματος
Η έννοια του άθροισμα προϊόντων (SOP) περιλαμβάνει κυρίως minterm, τύπους SOP, K-map και σχηματικό σχεδιασμό του SOP. Ομοίως, το προϊόν των ποσών (POS) περιλαμβάνει κυρίως το μέγιστος όρος , τύποι προϊόν των ποσών , k-map και σχηματικός σχεδιασμός POS.
Τι είναι το άθροισμα του προϊόντος (SOP);
Η σύντομη μορφή του αθροίσματος του προϊόντος είναι SOP, και είναι ένα είδος Δυαδική άλγεβρα έκφραση. Σε αυτό, οι διαφορετικές εισόδους προϊόντων προστίθενται μαζί. Το προϊόν των εισόδων είναι Boolean λογικό AND ενώ το άθροισμα ή η προσθήκη είναι λογική OR Boolean. Προτού καταλάβουμε την έννοια του αθροίσματος των προϊόντων, πρέπει να γνωρίζουμε την έννοια του minterm.
ο ελάχιστη διάρκεια μπορεί να οριστεί ως, όταν οι ελάχιστοι συνδυασμοί εισόδων είναι υψηλοί τότε η έξοδος θα είναι υψηλή. Το καλύτερο παράδειγμα είναι η πύλη AND, οπότε μπορούμε να πούμε ότι οι ελάχιστοι όροι είναι συνδυασμοί εισόδων πύλης AND. Ο πίνακας αλήθειας του ελάχιστου όρου φαίνεται παρακάτω.
Χ | Γ | ΜΕ | Ελάχιστο όριο (m) |
0 | 0 | 0 | X’Y’Z ’= m0 |
0 | 0 | 1 | X'Y'Z = m1 |
0 | 1 | 0 | X’Y Z ’= m2 |
| 0 | 1 | 1 | X'YZ = m3 |
| 1 | 0 | 0 | XY’Z ’= m4 |
1 | 0 | 1 | XY’Z = m5 |
| 1 | 1 | 0 | XYZ »= m6 |
| 1 | 1 | 1 | XYZ = m7 |
Στον παραπάνω πίνακα, υπάρχουν τρεις είσοδοι, συγκεκριμένα τα X, Y, Z και οι συνδυασμοί αυτών των εισόδων είναι 8. Κάθε συνδυασμός έχει ένα minterm που καθορίζεται με το m.
Τύποι αθροίσματος προϊόντος (SOP)
ο άθροισμα προϊόντων είναι διαθέσιμο σε τρεις διαφορετικές μορφές που περιλαμβάνουν τα ακόλουθα.
- Κανονικό άθροισμα προϊόντων
- Μη κανονικό άθροισμα προϊόντων
- Ελάχιστο άθροισμα προϊόντων
1). Κανονικό άθροισμα προϊόντων
Αυτή είναι μια φυσιολογική μορφή SOP και μπορεί να σχηματιστεί με την ομαδοποίηση των minterms της συνάρτησης για την οποία το o / p είναι υψηλό ή αληθινό και ονομάζεται επίσης ως το άθροισμα των minterms. Η έκφραση του κανονικού SOP συμβολίζεται με άθροισμα σημείων (∑) και τα minterms στο βραχίονα λαμβάνονται όταν η έξοδος είναι αληθής. Ο πίνακας αλήθειας του κανονικού αθροίσματος του προϊόντος φαίνεται παρακάτω.
Χ | Γ | ΜΕ | φά |
0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Για τον παραπάνω πίνακα, το κανονική μορφή SOP μπορεί να γραφτεί ως F = ∑ (m1, m2, m3, m5)
Επεκτείνοντας την παραπάνω άθροιση μπορούμε να πάρουμε την ακόλουθη συνάρτηση.
F = m1 + m2 + m3 + m5
Αντικαθιστώντας τα minterms στην παραπάνω εξίσωση μπορούμε να πάρουμε την παρακάτω έκφραση
F = X'Y'Z + X'YZ '+ X'YZ + XY'Z
Ο όρος προϊόντος της κανονικής μορφής περιλαμβάνει συμπληρωματικές και μη συμπληρωματικές εισόδους
2). Μη κανονικό άθροισμα προϊόντων
Στο μη κανονικό άθροισμα της μορφής προϊόντος, οι όροι προϊόντων απλοποιούνται. Για παράδειγμα, ας πάρουμε την παραπάνω κανονική έκφραση.
F = X'Y'Z + X'YZ '+ X'YZ + XY'Z
F = X'Y'Z + X'Y (Z '+ Z) + XY'Z
Εδώ Z ’+ Z = 1 (Τυπική λειτουργία)
F = X'Y'Z + X'Y (1) + XY'Z
F = X'Y'Z + X'Y + XY'Z
Αυτό εξακολουθεί να έχει τη μορφή SOP, αλλά είναι η μη κανονική μορφή
3). Ελάχιστο άθροισμα προϊόντων
Αυτή είναι η πιο απλοποιημένη έκφραση του αθροίσματος του προϊόντος και είναι επίσης ένας τύπος μη κανονικού. Αυτός ο τύπος κουτιού απλοποιείται με την αλγεβρική Boolean θεωρήματα αν και γίνεται απλά χρησιμοποιώντας K-map (χάρτης Karnaugh) .
Αυτή η φόρμα επιλέγεται λόγω του αριθμού των γραμμών εισαγωγής & χρησιμοποιούνται πύλες σε αυτό είναι ελάχιστο. Είναι κερδοφόρα χρήσιμο λόγω του συμπαγούς μεγέθους του, της γρήγορης ταχύτητάς του, καθώς και της χαμηλής τιμής κατασκευής.
Ας πάρουμε ένα παράδειγμα λειτουργίας κανονικής φόρμας και το ελάχιστο Σύνολο προϊόντων K χάρτη είναι

SOP K-χάρτης
Η έκφραση αυτού βάσει του χάρτη K θα είναι
F = Y'Z + X'Y
Σχηματικός Σχεδιασμός Αθροίσματος Προϊόντος
Η έκφραση του αθροίσματος του προϊόντος εκτελεί σχεδιασμό AND-OR δύο επιπέδων και αυτός ο σχεδιασμός απαιτεί μια συλλογή από πύλες AND και μία πύλη OR. Κάθε έκφραση του αθροίσματος του προϊόντος έχει παρόμοιο σχεδιασμό.

Σχηματικός σχεδιασμός του SOP
Ο αριθμός των εισόδων και ο αριθμός των πυλών AND εξαρτώνται από την έκφραση που εφαρμόζει. Ο σχεδιασμός για ένα ελάχιστο άθροισμα προϊόντος και κανονικής έκφρασης χρησιμοποιώντας πύλες AND-OR φαίνεται παραπάνω.
Τι είναι ένα προϊόν αθροίσματος (POS);
Η σύντομη μορφή του προϊόντος του αθροίσματος είναι POS και είναι ένα είδος έκφρασης άλγεβρας Boolean. Σε αυτό, είναι μια μορφή στην οποία λαμβάνονται προϊόντα του ανόμοιου αθροίσματος εισόδων, τα οποία δεν είναι αριθμητικά αποτελέσματα και άθροισμα αν και είναι λογικά Boolean AND & OR αντίστοιχα. Πριν κατανοήσουμε την έννοια του προϊόντος του αθροίσματος, πρέπει να γνωρίζουμε την έννοια του μέγιστου όρου.
Το maxterm μπορεί να οριστεί ως ένας όρος που ισχύει για τον υψηλότερο αριθμό συνδυασμών εισόδου, διαφορετικά είναι ψευδής για συνδυασμούς μεμονωμένων εισόδων. Επειδή η πύλη OR παρέχει επίσης λάθος για έναν μόνο συνδυασμό εισόδου. Έτσι, ο Max όρος είναι OR οποιασδήποτε συμπληρωμένης κατά τα άλλα μη συμπληρωμένων εισόδων.
Χ | Γ | ΜΕ | Μέγιστη διάρκεια (M) |
0 | 0 | 0 | X + Y + Z = M0 |
| 0 | 0 | 1 | X + Y + Z '= M1 |
0 | 1 | 0 | X + Y ’+ Z = M2 |
| 0 | 1 | 1 | X + Y ’+ Z’ = M3 |
1 | 0 | 0 | X ’+ Y + Z = M4 |
| 1 | 0 | 1 | X ’+ Y + Z’ = M5 |
1 | 1 | 0 | X ’+ Y’ + Z = M6 |
| 1 | 1 | 1 | X ’+ Y’ + Z ’= M7 |
Στον παραπάνω πίνακα, υπάρχουν τρεις είσοδοι, δηλαδή X, Y, Z και οι συνδυασμοί αυτών των εισόδων είναι 8. Κάθε συνδυασμός έχει έναν μέγιστο όρο που καθορίζεται με το M.
Σε μέγιστο όρο, κάθε είσοδος συμπληρώνεται καθώς παρέχει μόνο «0» ενώ εφαρμόζεται ο δηλωμένος συνδυασμός και η συμπλήρωση του minterm είναι ένας μέγιστος όρος.
M3 = m3 »
(X'YZ) '= M3
X + Y ’+ Z’ = M3 (Νόμος του De Morgan)
Τύποι προϊόντων αθροισμάτων (POS)
Το προϊόν του αθροίσματος ταξινομείται σε τρεις τύπους που περιλαμβάνουν τα ακόλουθα.
- Κανονικό προϊόν των αθροισμάτων
- Μη κανονικό προϊόν των αθροισμάτων
- Ελάχιστο προϊόν αθροισμάτων
1). Κανονικό προϊόν αθροίσματος
Το κανονικό POS ονομάζεται επίσης ως προϊόν μέγιστου όρου. Αυτά είναι AND από κοινού για τα οποία το o / p είναι χαμηλό ή ψευδές. Η έκφραση αυτή δηλώνεται με ∏ και οι μέγιστοι όροι στο αγκύλη λαμβάνονται όταν η έξοδος είναι λανθασμένη. Ο πίνακας αλήθειας του κανονικού προϊόντος του αθροίσματος φαίνεται παρακάτω.
Χ | Γ | ΜΕ | φά |
| 0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Για τον παραπάνω πίνακα, το κανονικό POS μπορεί να γραφτεί ως F = ∏ (M0, M4, M6, M7)
Με την επέκταση της παραπάνω εξίσωσης μπορούμε να πάρουμε την ακόλουθη συνάρτηση.
F = M0, M4, M6, M7
Αντικαθιστώντας τους μέγιστους όρους στην παραπάνω εξίσωση μπορούμε να πάρουμε την παρακάτω έκφραση
F = (X + Y + Z) (X ’+ Y + Z) (X’ + Y ’+ Z) (X’ + Y ’+ Z’)
Ο όρος προϊόντος της κανονικής μορφής περιλαμβάνει συμπληρωματικές και μη συμπληρωματικές εισόδους
2). Μη κανονικό προϊόν αθροίσματος
Η έκφραση του προϊόν αθροίσματος (POS) δεν είναι σε κανονική μορφή ονομάζεται μη κανονική μορφή. Για παράδειγμα, ας πάρουμε την παραπάνω έκφραση
F = (X + Y + Z) (X ’+ Y + Z) (X’ + Y ’+ Z) (X’ + Y ’+ Z’)
F = (Y + Z) (X ’+ Y + Z) (X’ + Y ’+ Z’)
Παρόμοιοι αν και οι αντίστροφοι όροι καταργούν από δύο μέγιστους όρους και φόρμες μόνο όρο για να τον δείξει εδώ είναι μια περίπτωση.
= (X + Y + Z) (X ’+ Y + Z)
= XX ’+ XY + XZ + X’Y + YY + YZ + X’Z + YZ + ZZ
= 0 + XY + XZ + X'Y + YY + YZ + X'Z + YZ + Z
= X (Y + Z) + X '(Y + Z) + Y (1 + Z) + Z
= (Y + Z) (X + X ’) + Y (1) + Z
= (Υ + Ζ) (0) + Υ + Ζ
= Υ + Ζ
Η παραπάνω τελική έκφραση εξακολουθεί να έχει τη μορφή Product of Sum ωστόσο, είναι με τη μορφή μη κανονικού.
3). Ελάχιστο προϊόν αθροισμάτων
Αυτή είναι η πιο απλοποιημένη έκφραση του προϊόντος του αθροίσματος και είναι επίσης ένας τύπος μη κανονικού. Αυτός ο τύπος κονσέρβας απλοποιείται με τα αλγεβρικά θεωρήματα Boolean αν και γίνεται απλά χρησιμοποιώντας το K-map (χάρτης Karnaugh).
Αυτή η φόρμα επιλέγεται λόγω του αριθμού των γραμμών εισαγωγής και οι πύλες που χρησιμοποιούνται σε αυτό είναι ελάχιστο. Είναι κερδοφόρα χρήσιμο λόγω του συμπαγούς μεγέθους του, της γρήγορης ταχύτητάς του, καθώς και της χαμηλής τιμής κατασκευής.
Ας πάρουμε ένα παράδειγμα της συνάρτησης κανονικής φόρμας και του Προϊόν των χαρτών αθροισμάτων Κ είναι

POS K-χάρτης
Η έκφραση αυτού βάσει του χάρτη K θα είναι
F = (Y + Z) (X '+ Y')
Σχηματικός σχεδιασμός προϊόντος αθροίσματος
Η έκφραση του προϊόντος του αθροίσματος εκτελεί δύο επίπεδα σχεδιασμού OR- AND και αυτός ο σχεδιασμός απαιτεί μια συλλογή από πύλες OR και μία πύλη AND. Κάθε έκφραση του προϊόντος του αθροίσματος έχει παρόμοιο σχεδιασμό.

Σχηματικός Σχεδιασμός POS
Ο αριθμός των εισόδων και ο αριθμός των πυλών AND εξαρτώνται από την έκφραση που εφαρμόζει. Η σχεδίαση για ένα ελάχιστο άθροισμα προϊόντος και κανονικής έκφρασης χρησιμοποιώντας πύλες OR-AND φαίνεται παραπάνω.
Επομένως, αυτό είναι όλο Κανονικές μορφές : Άθροισμα προϊόντων και προϊόν αθροίσματος, σχηματικός σχεδιασμός, χάρτης K, κ.λπ. Από τις παραπάνω πληροφορίες επιτέλους, μπορούμε να συμπεράνουμε ότι μια έκφραση Boolean αποτελείται εξ ολοκλήρου από οποιοδήποτε minterm αλλιώς το maxterm ονομάζεται κανονική έκφραση. Εδώ είναι μια ερώτηση για εσάς, ποιες είναι οι δύο μορφές κανονικών εκφράσεων;